Atom- und Astrophysik

Der folgende Überblick ist eine Zusammenfassung des siebenteiligen Kurses "Mikro- und Makrokosmos - Eine fächerübergreifende Einführung in die Atom- und Astrophysik", welcher von Regina Reuschl und mir im Physikalischen Verein Anfang 2006 gehalten wurde.

Motivation

Die Astrophysik untersucht die Objekte des Universums. Sie ist eine passive Wissenschaft und erhält ihre Informationen nicht durch Vor-Ort Experimente, sondern fast ausschließlich durch Beobachtung elektromagnetischer Strahlung. Licht (und auch andere elektromagnetische Strahlung) wechselwirkt dabei auf eine vor allem durch die Atomphysik beschriebene Weise mit Materie. Versteht man die atomphysikalischen Prozesse und weiss man, wo sie im Weltall auftreten, kann man durch diese Kenntnis viele Eigenschaften dieser Objekte ableiten.

Das Verhalten der uns umgebenden Materie wird bestimmt durch die vier Grundkräfte: Gravitation, Elektromagnetismus, Starke Kraft und Schwache Kraft. Die Atomphysik untersucht das Verhalten elektrisch geladener Teilchen unter dem Einfluß der Elektromagnetischen Kraft. Traditionell wird insbesondere die Wechselwirkung zwischen Protonen und Elektronen in Atomen beobachtet, seltener auch exotischere Atome. Es ist die Atomphysik, deren Prozesse die Farben des Universums bestimmen.

Wechselwirkungen zwischen Strahlung und Materie

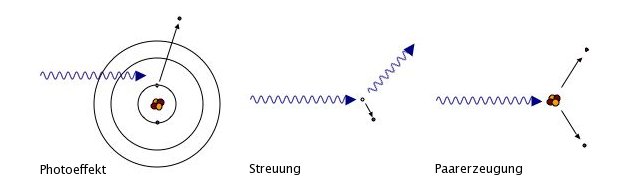
Es gibt nur 3 prinzipielle Klassen der Wechselwirkung zwischen Strahlung und Materie: Der Photoelektrische Effekt, für dessen Beschreibung Albert Einstein 1921 den Nobelpreis erhielt, Streuprozesse und Paarerzeugung. Alle anderen Prozesse werden jeweils einer dieser 3 Klassen zugeordnet.

Der Photoelektrische Effekt

Der hauptsächliche, unter diesem Begriff verstandene Effekt entspricht genau genommen der Photoionisation. Dabei wird die Energie des Photons komplett auf ein Elektron übertragen, welches dann das Atom verläßt (Ionisation). Daneben gibt es aber noch weitere Effekte, die dieser Klasse zugeordnet werden können, etwa Photoabsorbtion (In der Umkehr: Emission) und Auger-Effekt (Umkehr: Dielektronische Rekombination) sind Beispiele.

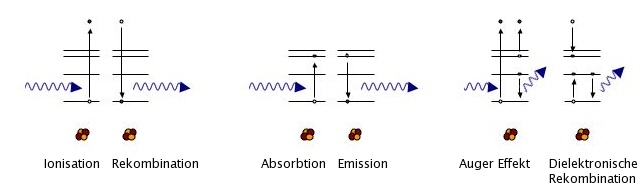
Die dem Photoelektrischen Effekt zugeordneten Vorgänge haben alle gemeinsam, daß sie alle zwischen dem Photon und dem Atom als Ganzes stattfinden. Aus Gründen der Energie- Impulserhaltung kann niemals ein einzelnes Photon von einem einzelnen Elektron absorbiert werden, sondern es nimmt immer auch der Atomkern teil. Gäbe es lediglich zwei freie Parameter, könnte das Photon niemals vollständig absorbiert werden, sondern es würde - da sich die Gleichungen der Impuls- und Energieerhaltung niemals ausgleichen - immer eine Restenergie übrigbleiben, die in Form eines Photons weiterliefe. In diesem Fall spräche man von Streuung.

Der Atomaufbau

Um die Spuren des Photoeffektes in den Spektren der Himmelskörper richtig zu verstehen, müssen wir nun den Atomaufbau verstehen. Eine Reihe von Quantenzahlen beschreibt die genaue "Form" der Atomhüllen. Diese können bereits in einem semiklassischen Bild veranschaulicht werden. Wirklich beeindruckend ist, daß die Konsequenzen aus diesen Modellen - sei es der Einfluß eines Magnetfeldes, Druck oder der Temperatur in der makroskopischen Welt beobachtet werden können und wertvolle Hinweise auf die Umgebungsbedingungen auf den entsprechenden Himmelskörpern liefern.

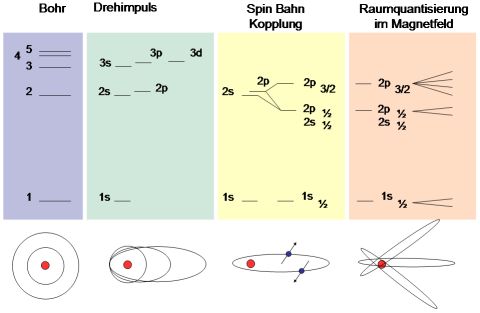
Ein einfaches Modell, welches bereits die wichtigsten Eigenschaften der Quantenwelt berücksichtigt, ist das Bohr-Sommerfeldsche Atommodell. In ihm umkreisen negativ geladene Elektronen einen positiv geladenen Atomkern. Bemerkenswert ist, daß sich die möglichen Bahnen der Elektronen nicht beliebig verteilen, sondern durch die Theorie genau vorhergesagt werden. Die Situation ist vergleichbar mit Flugzeugen, welche sich ausschließlich auf bestimmten Flugebenen bewegen, dabei von Ebene zu Ebene springen dürfen, nie jedoch in den Zwischenbereichen beobachtet werden.

Haupt- und Drehimpuls- und Magnetquantenzahlen

Den Bahnradien des Bohrschen Atommodells entspricht die Hauptquantenzahl n. Sie läuft von n=1 bis unendlich. Allerdings ist sie nicht die einzige Quantenzahl zur Charakterisierung der Elektronen im Potential des Atomkernes. Die Lösung der stationären Schrödingergleichung (siehe weiter unten) führt u.a. zur Drehimpulsquantenzahl l, einem Analogon des klassischen Drehimpulses, z.B. demjenigen der Planeten. Möchte man sich ein einfaches Bild von dieser Quantenzahl machen, so kann man sich elliptische Elektronenbahnen mit gleichem mittleren Abstand, jedoch unterschiedlich starker Ausprägung der Ellipse vorstellen.

Eine weitere Lösung der Schrödingergleichung führt zur Quantenzahl m. Die Interpretation dieser Quantenzahl ist die Raumlage der Elektronenbahnen. Diese wird allerdings erst meßbar, wenn eine Raumrichtung durch ein Kraftfeld ausgezeichet wird, z.B. ein magnetisches. Auf Bahnen bewegte Elektronen entsprechen einem Kreisstrom und damit einem Elektromagneten. Dieses Feld und damit die Bahnebene kann sich gegenüber des äußeren Magnetfeldes ausschließ in diskreten, also quantisierten, Richtungen anordnen. m entspricht demnach einer Raumqauntisierung.

Der Spin

Auf der Suche nach einem Nachweis für die Raumquantisierung der Elektronenbahnen entwickelten Stern und Gerlach in Frankfurt eine Apparatur, welche m auf Photofilm sichtbar machen sollte. Dafür schossen sie Silberionen durch ein inhomogenes Magnetfeld auf einen Photofilm. Dabei erbrachten Sie, ohne es zu zunächst zu wissen, den Nachweis für eine weitere, diesmal halbzahlige, Quantenzahl: Den Spin des Elektrons s. Der Spin kann, wie auch der Drehimpuls 2l+1 bzw. 2s+1 Werte annehmen. Für den halbzahligen Spin ergeben sich damit zwei Ausrichtungen: +1/2 und -1/2. Genau diese Ausrichtungen machten sich als zwei Streifen auf dem Photofilm bemerkbar. Erwartet hatten Stern und Gerlach drei Streifen, gemäß 2l+1, also 3 möglichen Ausrichtungen bei einem Elektron mit l=1, vorhergesagt durch Theorie der Silberionen.

Die Quantenzahlen im Überblick:

• n = 1, 2, 3, ... (Hauptquantenzahl)
• l = 0, 1, ..., n-1 (Nebenquantenzahl / Drehimpulsquantenzahl)
• m = - (2l+1), -2l, ..., +2l, 2l+1 (Magnetquantenzahl)
• s = - 1/2, + 1/2 (Spin)

Energieveaus in einfachen Atomen

Wir betrachten zunächst Wasserstoffähnliche Systeme, d.h. Atome mit nur einem Elektron. Diese können durch ausreichende Ionisation aus allen Elementen hergestellt werden. So entspricht etwa das 91 fach ionisierte Blei mit nur einem Elektron bis auf eine Energieskalierung durch die höhere Kernladung dem Funktionsprinzip des Wasserstoffs.

Es liegt auf der Hand, daß Körper im Falle eines Absturzes einen besonders großen Knall erzeugen, wenn sie aus großer Höhe fallen. Dementsprechend können wir auch Elektronen je nach "Flugebene" eine entsprechende potentielle Energie zuordnen. Flugebenen entsprechen bei den Elektronen der Hauptquantenzahl n, daher wird die Energie insbesondere von dieser Quantenzahl abhängen. Ein Elektron mit n = 3 "fliegt" höher um den Atomkern als ein Elektron mit n = 1, daher hat es auch eine höhere Energie. Doch es ist nicht ganz so einfach, denn auch die anderen, eben eingeführten Quantenzahlen l, s und m, spielen für die tatsächliche Energie der Elektronenbahnen eine wesentliche Rolle.

Koppelnder Spin und Drehimpuls

Durch Messungen der Energien kann man zeigen, daß sich die Drehimpuls- und die Spinquantenzahl addieren. Man spricht in diesem Zusammenhang auch von " koppeln". Ein Elektron mit einer Drehimpulsquantenzahl von l = 1 und einem Spin s = 1/2 besitzt demnach eine neue Quantenzahl von (nennen wir sie j) j = 3/2, denn 1 + 1/2 = 3/2. Hat das Elektron ein Drehimpuls l = 1, jedoch einen negativen Spin s = - 1/2 , sowird der Spin vom Drehimpuls abgezogen. Wir kommen auf eine neue Quantenzahl von j = 1/2 , denn 1 - 1/2 = 1/2

Die Energien von Elektronen gleicher Hauptquantenzahl n und gleichem j sind dieser Theorie nach identisch. In der konkreten Anwendung bedeutet dies, daß ein Elektron mit l = 2 und s = 1/2 (also mit einem j = 5/2) die gleiche Energie aufweist, wie ein Elektron mit l = 3 und s = - 1/2 (also auch j = 5/2). Man spricht von "Entartung". Dieses Verhalten der Energien beschreibt bereits sehr gut die sogenannte "Feinstrukturaufspaltung" in den Atomen, die bei sehr genauer Betrachtung von Spektren (z.B. demjenigen der Sonne) aus Einzellinien eine Vielzahl feinerer Linen werden läßt.

Aufhebung der "Entartung"

In unseren Überlegungen zu der Energie der Elektronenbahnen haben wir bislang die Magnetquantenzahl m ausgelassen. Da Bewegung und Spin der Elektronen - vergleichbar mit einem Elektromagneten - ein magnetisches Feld (besser: Moment) erzeugen, wirkt auf die Elektronen ein weiteres Kraftfeld, sobald wir von außen ein starkes Magnetfeld anlegen. Ähnlich der Kopplung von Spin und Drehimpuls koppelt nun dieses magnetische Moment mit dem äußeren Feld und so spalten die Energien der Elektronen ein weiteres Mal auf. Die Entartung wird in diesem Fall aufgehoben. Nach der oben beschriebenen Regel kann die Bahn in 2l+1 unterschiedlichen Richtungen ausgerichtet sein (Raumquantisierung), und somit die Energie entsprechend ihrer Ausrichtung anheben oder verringern. Unter Berücksichtigung der eben beschriebenen Kopplung von Drehimpuls und Spin müssen wir - wenn man genauere Betrachtungen anstellen will - jedoch mit 2j+1 Energieaufspaltungen arbeiten. Dies macht sich jedoch erst im Magnetfeld bemerkbar.

Mehrelektronen-Systeme

Das Heliumatom mag an dieser Stelle als einfachstes Beispiel für ein Zwei - Elektronen System herhalten. Auch Helium - ähnliche Atome können durch ausreichende Ionisation aus allen Elementen hergestellt werden. Alle diese Systeme funktionieren dann - innerhalb gewisser Grenzen - nach den entsprechenden Regeln für Zweielektronen - Systeme. Daher sind die hier vorgestellten Eigenschaften für alle Mehrelektronensystem gültig.

In Mehrelektronen - Systemen koppeln Quantenzahlen mehrerer Elektronen miteinander. Die Kopplungsreihenfolge hängt von der Kernladungszahl Z ab, sodaß es Unterschiede in der Funktionsweise zwischen leichten und schweren Atomen gibt. Bei dem leichten Atomen gilt die Russel - Saunders Kopplung (auch LS-Kopplung genannt). Das heißt, es werden zunächst die Drehimpulsvektoren l1 + l2 beider Elektronen addiert, dann die Spinvektoren s1 + s2 und dann die beiden resultierenden Summenvektoren L + S miteinander. Um die jeweiligen Summenvektoren von den Einzelvektoren zu unterscheiden, werden sie mit Großbuchstaben gekennzeichnet. L = l1 + l2 und S = s1 + s2 sowie J = L+S.

Multiplett Linien

Man kann sich leicht vorstellen, daß die unterschiedlichen Ausrichtungen der vektoriellen Kopplungsmöglichkeiten zu verschiedenen Energienieveaus in den Mehrelektronen - Atomen führen. Wer ein wenig mit den Kopplungsmöglichkeiten spielt, wird feststellen, daß es genau 2J+1 unterschiedliche Möglichkeiten pro Hauptquantenzahlen sind. Ein Beispiel: Die Spins in der P-Schale von (Para)Helium können sich räumlich gesehen in 2s+1, also 1*1/2 + 1 = 2 Raumrichtungen ausrichten. Dann können beide nach oben zeigen, beide nach unten, oder beide in unterschiedliche Richtungen. Es ergeben sich also 3 Ausrichtungsmöglichkeiten gegenüber dem Drehimpuls-Vektor und wir beobachten ein Linientriplett. Es gibt allerdings auch die Möglichkeit daß sich die beiden Spins durch ihre Ausrichtung im Raum vollständig annihilieren. Diesen Singulettzustand unterscheidet man vom Triplett - Zustand. Man nennt dieses Heliumatom dann auch (Ortho)Helium. Da für den Übergang aus dem Para- in den Ortho- Zustand ein eher seltener Spinflip notwendig ist, dachte man früher sogar, daß es sich bei Ortho- und Parahelium um zwei völlig unterschiedliche Systeme handelt, die nicht ineinander überführt werden können.

Um die Linien der auf diese Kopplungsweise zustandegekommenen Zustände zu identifizieren schreibt man Hauptquantenzahl sowie die vektoriell addierte Drehimpulsquantenzahl L hintereinander. Hinter das L stellt man tiefgestellt das Gesamt - J. Da es für dieses J - wie wir gesehen haben - genau 2S + 1 Möglichkeiten gibt, schreibt man dieses hochgestellt vor den Drehimpuls. 2 * (1/2 + 1/2 ) + 1 wäre 3 und steht führ die Triplett Linien, 2 * (1/2 - 1/2) + 1 ist 1 und steht daher für unseren Singulett Zustand.

Atomare Übergänge

Durch die Emission oder die Absorbtion von Licht kommt es zu Sprüngen der Elektronen zwischen den einzelnen Orbitalen (Anregung / Abregung). Da die Photonen einen Drehimpuls von +-1 besitzen, muß dieser beim Emissions- oder Absorbtionsprozess ausgeglichen werden. Aus diesem Grund muß sich neben der Energie auch der Gesamtdrehimpuls des Atoms ändern.

In den allermeisten Fällen geschieht dies durch eine Änderung des Bahndrehimpulses des Elektrons und damit der Elliptizität der Elektronenbahn. Bei diesem Vorgang, dem elektrischen Dipolübergang (E1), entspricht die Wahrscheinlichkeit, das Photon in einer bestimmten Richtung zu emittieren, der typischen Strahlungskeule einer Dipolantenne. Um den Drehimpuls des Photons auszugleichen, sind jedoch auch andere Prozesse denkbar, etwa eine Umkehrung des Elektronenspins. Dieser wesentlich seltenere Prozess, bei dem es nun keine Änderung der Drehimpulsquantenzahl mehr gibt, führt zum sogenannten Magnetischen Dipolübergang (M1).

Ein noch exotischeres Beispiel ist die gleichzeitige Emission von zwei Photonen mit entgegengesetztem Drehimpuls (2E1). Es gibt noch viele weitere solcher "Ordnungen", für die es jeweils unterschiedliche Abstrahlcharakteristiken gibt. Auch kann etwa die Polarisation, der bei den unterschiedlichen Übergängen emittierten Strahlung sehr unterschiedlich sein. Die Regeln, aus denen sich erkennen läßt, welche Veränderung von Quantenzahlen zu welchem Übergang führt nennen sich Auswahlregeln

Verbotene Linien

Der unter normalen Bedingungen fast auschließlich vorzufindendende Übergang ist der Elektrische Dipolübergang E1. Alle anderen Übergänge sind so selten, daß die mittlere Zeitdauer (Halbwertszeit), die man warten muß, um einen solchen Übergang zu beobachten extrem lang ist. Daher regen sich Zustände, die sich aufgrund der Auswahlregeln nur über solche Übergänge bewegen können, weit häufiger über Stoßprozesse mit Nachbaratomen ab, als durch die Emission von Lichtquanten.

Im Weltall jedoch beobachtet man solche Prozesse zum Beispiel in Planetarischen Nebeln, wo die Teilchendichten so niedrig sind, daß keine Stoßabregung mit benachbarten Atomen möglich ist. Hier werden die Atome sozusagen "gezwungen", in einem dieser seltenen Prozesse Licht zu emittieren. Tatsächlich sind diese Übergänge auf der Erde unter normalem Luftdruck kaum zu beobachten, wesshalb William Huggins nach der ersten erfogreichen spektroskopischen Beobachtung eines Planetarischen Nebels (1864) die Existenz eines bislang unbekannten Elementes postulierte, dem sogenannten "Nebulium". Nach langer Zeit wurde das Rätsel schließlich 1927 von Ira Bowen gelöst, indem er nachwies, daß es sich bei diesen Linien um die verbotenen Linien des zweifach ionisierten Sauerstoffs [OIII] handelte, die man auch in speziellen Bogenentladungslampen oder in den Polarlichtern beobachten kann.

Wellenmodelle der Quantenmechanik

An dieser Stelle sollte darauf hingewiesen werden, daß der bisher verwendete Begriff der Elektronenbahn in Wirklichkeit so nicht vorkommt. Obwohl nur bestimmte, genau festgelegte Energien der Elektronen vorkommen, ist der Ort eines Teilchens nicht genau bestimmt. Dies ist die Unschärferelation, die besagt, daß wir entweder die Energie oder den Ort eines Teilchens bestimmen können. Wenn wir also eine Messung der Energie vornehmen (und dies machen wir, wenn wir Farben / Spektren betrachten), so wird der Aufenthaltsort der Elektronen verschmiert. Für spektroskopische Beobachtungen ist es also sinnvoll, sich ein verschmiertes Gebiet der Aufenthaltswahrscheinlichkeiten vorzustellen.

Es stellt sich heraus, daß es sinnvoll ist diese Aufenthaltswahrscheinlichkeiten der Elektronen in Form einer Überlagerung von Wellen zu beschreiben. Ganz analog zu akkustischen Schwingungen, die man auf einem Oszilloskop oder einem Bildschirm in Wellenform aufzeichnet. Dabei ist es bemerkenswert, daß man in der Akkustik durch eine Überlagerung verschiedenster Frequenzen und Amplituden alle möglichen Wellenformen produzieren kann. So z.B. eine Sägezahnschwingung oder - noch viel überraschender - auch nicht-periodische Signale aus einer geschickten Überlagerung ursprünglich periodischer Cosinus und Sinus Wellen - z.B. einen Knall.

In der Atomphysik überlagern wir nach dem gleichen Prinzip Wahrscheinlichkeitswellen. Diese kann man sich wie Wasserwellen vorstellen, nur daß die Orte der Wellenberge und -täler für besonders hohe Aufenthaltswahrscheinlichkeiten der Elektronen stehen. Damit es keine negativen Aufenthaltswahrscheinlichkeiten gibt, ist die eigentliche Aufenthaltswahrscheinlichkeit genau genommen durch das Quadrat der Wellenfunktion gegeben. Hierdurch sind negative Vorzeichen in jedem Fall ausgeschlossen. In dieser Darstellungsweise besteht ein Elektron also aus einer verschmierten, jedoch geschickt gewählten Überlagerung vieler Einzelwellen verschiedener Frequenzen und Amplituden. In dieser (durchaus sinnvollen) Wahl der Darstellungsweise liegt auch die Ursache für die oft mystifizierte Komplexe Darstellungsweise der Quantenmechanik. Dabei ist die Komplexe Berechnung nichts anderes als ein Rechentrick um die Phaseninformation (also die Abstände der Wellen) leichter aufzuschreiben. Und dass die Phaseninformation bei Überlagerungen von Wellen von Bedeutung sein wird, liegt klar auf der Hand.

Ein Elektronenobital besteht also aus einer Überlagerung von vielen Einzelwellen, welche die verschmierte Aufenthaltswahrscheinlichkeit des Elektrons beschreiben. Ein Atomorbital ergibt sich dann aus der Reaktion der Gesamtwellenfunktion der Elektronen auf das Zentralpotential des Atoms.

Chemische Verbindungen

Fluoreszenz / Phosphorenszenz

Fluorszente Materialien absorbieren energiereiche elektromagnetische Strahlung und emittieren weniger energiereiche Strahlung. Besonders eindrucksvoll ist dies, sofern dabei für den Beobachter unsichtbare UV Strahlung in visuell wahrnehmbare Strahlung umgewandelt wird. Die betroffenen Materialien erscheinen für den Beobachter "von selbst" zu leuchten oder wirken zumindest heller , als sie es bei den gegebenen Beleuchtungsverhältnissen sein sollten. Besonders in den 80er und 90er Jahren wurden Neonfarben daher gerne genutzt. Farbe von Textmarkern, die auf diese Weise funktioniert, wurden in obigem Beispiel näher analysiert. Bei dem Vorgang können auch spinverbotene Übergänge genutzt werden, bei denen sich der Übergang verzögert so dass diese Materialien noch lange Zeit nachleuchten (Phosphoreszenz, siehe unteres Spektrum).

Im Gegensatz zu den bislang besprochenen atomaren Systemen handelt es sich bei den in Textmarkern verwendeten Farbstoffen um chemische Verbindungen. Beispielsweise bei der besonders eindrucksvollen Neongelb - Farbe um die Natrium - Salze des Fluoreszins, dem sogenannten Uranin. Die hier abgebildete Fluoreszenz findet also in einem System statt, welches - verglichen mit Atomen - Energie auch über zusätzliche Schwingungen und Rotationen aufnehmen kann. Die eigentliche Energieverschiebung zwischen UV - Absorbtion und visueller Emission, der sonannten "Stokes - Verschiebung" wird dabei durch das bei Molekülen wichtige Franck - Condon Prinzip hervorgerufen:

Die innerhalb der elektronischen Energieniveaus unterschiedlichen vibronischen Energieniveaus, werden durch den molekularen Potentialtopf bestimmt, der sich jedoch bei einer elektronischen Anregung durch die Änderung des Abstands zwischen Elektron und Kernen ebenfalls verschiebt. Der Überlapp der vibronischen Wellenfunktionen der elektronischen Grundfunktion im Ursprungszustand und den angeregten vibronischen Zuständen im verschobenen Potential ist wegen dieser Verschiebung größer als die Überlappung der jeweiligen Grundfunktionen. Daher muss es bei einer elektronischen Anregung ebenfalls zu einer vibronischen Anregung kommen.

Sind Elektron und passender Schwingungszustand erst angeregt, erfolgt die Abregung zwischen den vibronischen Zuständen zumeist über mehrere ggf. nicht visuell nachweisbare vibronische Zwischenschritte. Bis die wahrscheinlichsten Übergänge zwischen dem elektronisch angeregten Molekül und dem elektronischen Grundzustand stattfinden, führt die Energiedifferenz bei der vibronischen Abregungskaskade zu der Stokes - Verschiebung aus dem UV Bereich in den visuellen Bereich des elektromagnetischen Spektrums. Sind bei der finalen Abregung in den Grundzustand spinverbotene Übergänge im Spiel, verzögert sich die Abregung und man spricht von Phosphoreszenz. Während bei fluoreszierenden Gasen die entsprechenden Linien im Spektrum erkennbar sind, kommt es bei Flüssigkeiten oder Festkörpern zu einer starken Linienverbreiterung, so dass es wie in unseren Beispielen zu kontinuumsähnlichen Emssions- bzw. Absorbtionsgebieten kommt.

Literatur

T. Mayer-Kuckuk, Atomphysik, Teubner, Stuttgart 1997

K. Bethge, G. Gruber, T.Stoehlker, Physik der Atome und Moleküle, Wiley-VCH, 2004

W. Dermtröder, Experimentalphysik 3, Atome Moleküle Festkörper, Springer, 2005